ARTIGOS GERAIS

 

O método numérico de Numerov aplicado à equação de Schrödinger

 

Numerov numerical method applied to the Schrödinger equation

 

 

Francisco Caruso^{I, II, 1}; Vitor Oguri^II

^ILaboratório de Física Experimental de Altas Energias, Centro Brasileiro de Pesquisas Físicas, Rio de Janeiro, RJ, Brasil
^IIInstituto de Física Armando Dias Tavares, Universidade do Estado do Rio de Janeiro, Rio de Janeiro, RJ, Brasil

 

 

---

RESUMO

Neste artigo mostra-se como resolver numericamente problemas de autovalor associados a equações diferenciais ordinárias lineares de segunda ordem, contendo também termos que dependem da derivada primeira da variável incógnita. Nesse sentido, faz-se uma apresentação didática do método de Numerov e, em seguida, ele é aplicado a dois problemas clássicos da mecânica quântica não relativística cujas soluções analíticas são bem conhecidas: o oscilador harmônico simples e o átomo de hidrogênio. Os resultados numéricos são confrontados com os obtidos analiticamente.

Palavras-chave: método de Numerov, oscilador harmônico, átomo de hidrogênio, mecânica quântica.

---

ABSTRACT

In this paper it is shown how to solve numerically eigenvalue problems associated to second order linear ordinary differential equations, containing also terms which depend on the first derivative of the unknown variable. A didactic presentation of the Numerov Method is given and, in the sequel, it is applied to two quantum non-relativistic problems with well known analytical solutions: the simple harmonic oscillator and the hydrogen atom. The numerical results are compared to those obtained analytically.

Keywords: Numerov method, harmonic oscillator, hydrogen atom, quantum mechanics.

---

 

 

1. Introdução

A grande maioria dos métodos numéricos, como os de Newton, Euler, Lagrange, Gauss, Fourier, Jacobi, Runge-Kutta e tantos outros, foi introduzida no contexto das aplicações em física, astronomia ou em outras de natureza técnica, como na aerodinâmica [Benzi]. Desde então, a análise numérica não era reconhecida como uma disciplina matemática e tal situação perdurou durante as quatro primeiras décadas do século XX. Hoje, apesar de alguns métodos numéricos serem ensinados nos cursos de física, no âmbito de disciplinas da matemática, pouca ênfase é dada a eles nas aplicações físicas. Com a popularização dos computadores portáteis, cada vez mais acessíveis ao grande público, e capazes de executar tarefas cada vez maiores e mais complexas, parece um contrassenso não explorá-los no ensino de física e de engenharia.

O matemático húngaro Peter Lax, do Instituto Courant da Universidade de Nova Iorque, reforça a relevância do ensino dos métodos numéricos destacando, com muita propriedade, seu aspecto universal e a importância de os alunos explorarem soluções de equações diferenciais utilizando computadores [2]:

Métodos numéricos têm a grande virtude que se aplicam universalmente. Quando são introduzidos métodos especiais para lidar com a lamentavelmente pequena classe de equações [diferenciais] que podem ser tratadas analiticamente, os alunos estão aptos a perder de vista a ideia geral de que cada equação diferencial tem uma solução e que essa solução é determinada unicamente pelos dados iniciais. Que hoje podemos utilizar computadores para explorar as soluções de equações [diferenciais] é verdadeiramente revolucionário; estamos apenas começando a vislumbrar as consequências.²

Na confluência dessas duas tendências, procura-se divulgar aqui um poderoso método de cálculo numérico desenvolvido originalmente por Boris Vasil'evich Numerov [3-5], aplicando-o à equação de Schrödinger independente do tempo no caso de dois problemas típicos: o oscilador harmônico simples e o átomo de hidrogênio. Esses são bons exemplos didáticos, pois suas soluções analíticas são bem conhecidas.

O primeiro exemplo, para o qual se determina o espectro de energia do oscilador harmônico simples como um problema de autovalor, e as respectivas autofunções ψ(x), ou funções de onda, ilustra o comportamento de uma partícula em um poço de potencial unidimensional, quando a equação de Schrödinger não contém termos de derivada de primeira ordem.

No segundo exemplo, o qual envolve a equação de Schrödinger contendo termo de derivada primeira, uma variante do método original de Numerov será aplicada para se obter o espectro e a solução radial do átomo de hidrogênio.

Com esses exemplos, serão esboçados alguns detalhes do procedimento geral utilizado no cálculo da solução numérica de equações diferenciais de segunda ordem.

 

2. O método de Numerov

A motivação inicial de Numerov era poder calcular correções à trajetória do cometa Halley. Portanto, na prática, o método de Numerov foi desenvolvido, inicialmente, para determinar as soluções de problemas de autovalores associados a equações diferenciais ordinárias de 2a ordem da mecânica celeste, que não continham termos envolvendo a derivada primeira de uma função incógnita y(x), ou seja, equações da forma

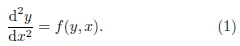
Toda equação do tipo (1) pode ser substituída pelo seguinte sistema de equações de primeira ordem ³

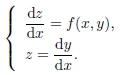
Os métodos tradicionais para resolver numericamente tal sistema de equações, como os de Euler ou de Runge-Kutta, consideram que os valores de y(x) e de dy/dx sejam conhecidos em um dado ponto do domínio [a,b] de validade do sistema, i.e., são adequados para os chamados problemas de valor inicial.

Em mecânica quântica não relativística, nos problemas de estados ligados que envolvem uma partícula de massa m confinada em um poço de potencial V(x), em um dado intervalo a<x<b, as energias permitidas (E) e as correspondentes funções de onda ψ(x) que descrevem esses estados estacionários satisfazem a equação de autovalor de Schrödinger

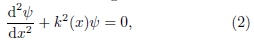
em que 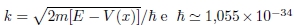J.s é a constante de Planck reduzida.

Nesses casos, como não se conhece o valor da derivada primeira da função de onda, os métodos de Euler e Runge-Kutta não podem ser empregados. Entretanto, é possível estabelecer condições de continuidade para os valores de ψ e dψ/dx em dois ou mais pontos do domínio da função de onda, o que caracteriza os chamados problemas de valor de contorno.

Além de tornar desnecessária a transformação de uma equação diferencial de segunda ordem em um sistema de primeira ordem, o método de Numerov permite a determinação simultânea do espectro de energia da partícula e das autofunções associadas a cada valor de energia.

Como todo método numérico iterativo, a solução da Eq. (2) é construída por integrações sucessivas, realizadas passo a passo, a partir de valores arbitrários para possíveis soluções em um ou mais pontos do domínio de integração.

Assim, no método de Numerov, inicialmente, considera-se que a solução seja conhecida em dois pontos subsequentes do intervalo [a,b], por exemplo, em ψ(x-δ) e ψ(x), sendo δ uma quantidade arbitrariamente pequena, denominada passo da integração. A seguir, procura-se estabelecer, então, um algoritmo numérico para se determinar a solução no ponto seguinte, ψ(x+δ).

O ponto de partida para estabelecer esse algoritmo é a expansão de ψ(x±δ) em séries de Taylor, até derivadas de quarta ordem, ou seja,

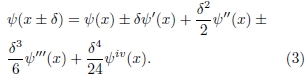
Somando-se os termos ψ(x+δ) e ψ(x-δ), apenas as derivadas de ordem par sobrevivem e, portanto, chega-se a uma relação entre os valores de uma função em três pontos e sua derivada segunda, dada por

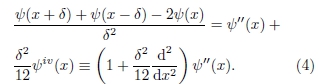
Escrevendo a equação de Schrödinger unidimensional, Eq. (2), na forma conveniente

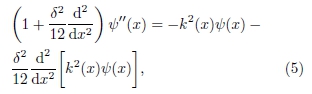
e utilizando a Eq. (4) para substituir os termos que contêm derivadas de segunda ordem, obtém-se

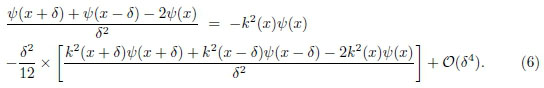
Reagrupando a Eq. (6), obtém-se a fórmula de diferenças de Numerov para o problema de uma partícula sob ação de um potencial unidimensional,

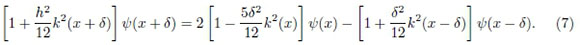
Na realidade, cabe notar que o algoritmo pode ser aplicado a qualquer equação diferencial ordinária linear e homogênea de segunda ordem que não contenha termos de derivada primeira.

Uma vez que o problema de interesse é um problema de autovalor, a técnica de integração numérica da equação unidimensional de Schrödinger para uma partícula em um poço depende de se associarem valores arbitrários convenientemente aos autovalores e às respectivas (possíveis) autofunções em 2 pontos do domínio do problema. Mas como fazê-lo? Com relação à escolha do valor inicial para a energia (primeiro autovalor), basta lembrar que, de acordo com a relação de incerteza de Heisenberg, a energia E de uma partícula em um poço de potencial V(x) deve ser maior que o valor mínimo do poço. Assim, considera-se, inicialmente, que E _inicial=V_min+ΔE, com ΔE>0.

A escolha de um valor para a energia determina 2 pontos, x_ℓ e x_r, nos quais o valor da energia é igual ao valor da energia potencial, e correspondem aos pontos de retrocesso de uma partícula cujo movimento obedece à mecânica clássica newtoniana. Ou seja, do ponto de vista da mecânica clássica, o movimento da partícula está restrito apenas à região [x_ℓ,x_r], na qual a energia é maior ou igual à energia potencial. As regiões x<x_ℓ e x>x_r são denominadas regiões classicamente proibidas, e estão assinaladas na Fig. 1.

 

 

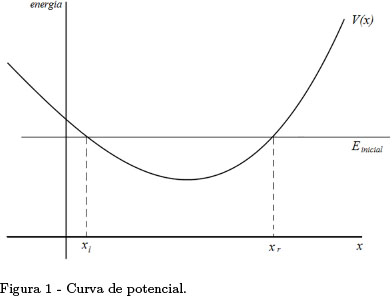
Como a equação de Schrödinger admite soluções para essas regiões classicamente proibidas, para cada valor de energia, inicialmente, se atribuem valores para uma possível autofunção em 2 pontos das regiões classicamente proibidas, nos quais a função ψ praticamente se anula. Em geral, esses são os pontos limites a e b>a do domínio de integração da função.

No entanto, a implementação do método de Numerov para a solução do problema ainda requer um esquema de iteração que utiliza a fórmula de Numerov em duas etapas: a partir de a, ou à esquerda de um dos pontos de retrocesso clássico, doravante denominado match point (x_match), e a partir de b, ou à direita do match point.

Desse modo, tomando-se arbitrariamente um valor inicial para a energia, e dois valores arbitrários sucessivos para a solução, a partir dos extremos inferior e superior do intervalo de integração [a,b], pode-se implementar o esquema de iteração do método nos dois sentidos, como:

1. Solução à esquerda do match point (x<x_match).

Seja E_inicial=V_min+ΔE (ΔE/|V_min|≪1) um valor arbitrário para a energia da partícula. Arbitrando-se também valores para a função de onda, em 2 pontos sucessivos, a partir de a,

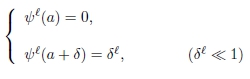
e utilizando-se a fórmula de diferenças, Eq. (7), a solução à esquerda é construída sequencialmente até o match point (x_match), em que ψ^ℓ(x_match)=ψ^ℓ_match.

2. Solução à direita do match point (x>x_match).

De maneira similar, para o mesmo valor E_inicial, arbitrando-se

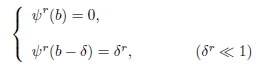
a solução à direita, a partir de b, é construída sequencialmente até os pontos x_match e x=x_match-δ, em que

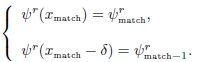
Para garantir a condição de contorno da solução, redefine-se a solução à esquerda conforme a Eq. (8) dada a seguir, e testa-se a condição de contorno das derivadas primeiras, segundo a Eq. (9).

O procedimento é repetido passo a passo, nos dois sentidos, . Partindo-se de a, utilizando-se a fórmula de recorrência de Numerov associada à equação, se constrói a solução ψ^ℓ até que se atinja o ponto de retrocesso clássico, por exemplo, mais próximo de b, no qual E=V(x_match), chamado de match point. Depois, a partir de b, faz-se o análogo, construindo-se a solução ψ^r até o match point. Em princípio, as possíveis soluções ψ^ℓ e ψ^r não serão necessariamente iguais neste ponto xmatch. Para assegurar a continuidade da solução redefine-se ψ^ℓ como

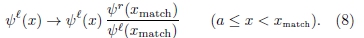
Finalmente, verifica-se quão próximos são os valores das respectivas derivadas primeiras de ψ^r e da nova função ψ^ℓ assim escalonada, no match point.

Para se testar a condição de contorno das derivadas primeiras, tendo-se em conta as séries de Taylor para ψ(x+δ) e ψ(x-δ), até a primeira ordem, pode-se escrever

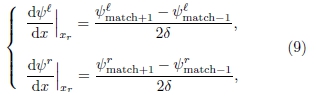
nas quais ψ_match±1=ψ(x_match±δ).

Se a diferença entre esses valores for menor que o valor de um erro predefinido, interrompe-se o processo, confirmando-se o autovalor procurado e a respectiva autofunção como sendo

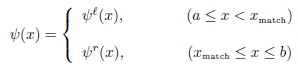
Se a condição de continuidade das derivadas não for satisfeita, incrementa-se o valor da energia para a busca de um novo valor, que seja realmente um autovalor do problema, e de sua respectiva autofunção.

O processo pode ser repetido até que se determine o número desejado de autovalores e autofunções do problema.

Por se basear na expansão em série de Taylor até quarta ordem, o erro no método de Numerov [7] é bem menor do que o erro em métodos baseados em expansão em ordem mais baixa, como o de Runge-Kutta.

 

3. O oscilador harmônico

A equação de Schrödinger para uma partícula de massa m em um campo conservativo, tal como um poço de potencial unidimensional V(x), pode ser escrita como uma equação de autovalor

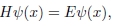
na qual as energias E são os autovalores e as funções ψ(x), as respectivas autofunções de quadrado integrável do operador hamiltoniano H dado por

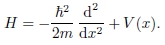
Considerando que um potencial físico real se anula no infinito, as autofunções também se anulam nos extremos de um dado intervalo [a,b] que será o domínio de integração da equação, i.e., ψ(a)=ψ(b)=0.

Assim, de um outro ponto de vista, o problema do poço unidimensional é um problema de autovalor que envolve uma equação diferencial linear e homogênea de segunda ordem do tipo

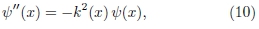
sujeita a condições de contorno nos limites de um intervalo [a,b], sendo

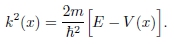
Um exemplo típico de um problema em mecânica quântica, que envolve a equação de Schrödinger sem termo de derivada primeira, é a determinação dos autovalores e autofunções do oscilador harmônico de massa m e frequência natural ω, cuja energia potencial é dada por

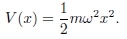
Assim, k²(x) pode ser escrito como

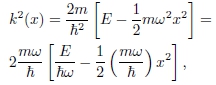
e a equação de Schrödinger pode ser escrita como

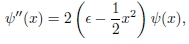
onde x está em unidades de 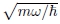e a energia ε, em unidades de ħω.

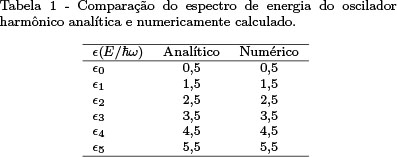
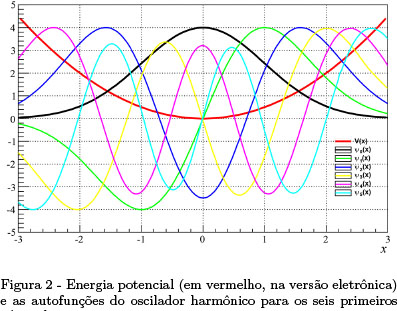
A Tabela 1 mostra a comparação dos 6 primeiros autovalores (ε) de um oscilador harmônico, calculados analítica e numericamente, em unidades de ħω, e a Fig. 2, as correspondentes autofunções, numericamente determinadas, em função de x, onde x está em unidades de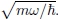

 

 

 

 

4. O átomo de hidrogênio não relativístico

Apesar de ter sido desenvolvido para equações diferenciais ordinárias lineares e homogêneas de segunda ordem que não contenham termos de derivada primeira, o método de Numerov pode ser generalizado para abranger a presença de termos que contenham derivada primeira na equação diferencial, de modo a se poder considerar também problemas de autovalor [8].

De fato, no caso de equações lineares, toda equação diferencial de segunda ordem do tipo

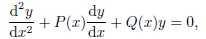
pode ser escrita em sua forma normal [9]

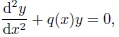
onde

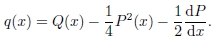
A equação radial de Schrödinger para uma partícula de massa m sob a ação de um campo elétrico coulombiano, como o elétron no átomo de hidrogênio, pode ser escrita como

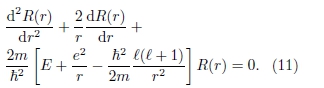
Fazendo-se a substituição de variável r=xa_B, sendo a_B=ħ²/(me²) o raio de Bohr, pode-se reescrever a equação diferencial anterior, Eq. (11), para uma nova função y(x)=R(r), como uma equação de autovalor

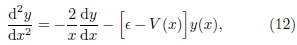
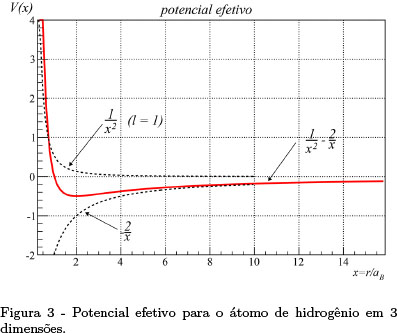
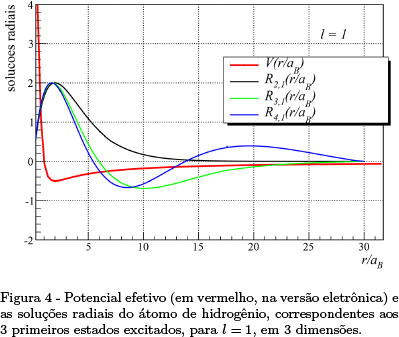
em que ε= E/e²/(2a_B) e V(x)= ℓ(ℓ+1)/x² - 2/x são, respectivamente, a energia e o chamado potencial efetivo (Fig. 3), em unidades atômicas.

 

 

Nesse caso, a equação que se pretende resolver pelo método de Numerov apresenta um termo que envolve a derivada primeira, e pode ser expressa por

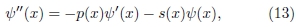
onde

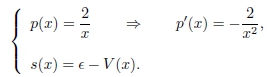
De acordo com as expansões de Taylor, Eq. (3), pode-se reescrever a Eq. (13) como

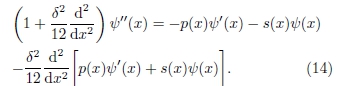
De maneira similar ao caso anterior, de acordo com a Eq. (4), pode-se escrever o termo do lado direito da Eq. (14) que contém derivadas de ordem 2, como

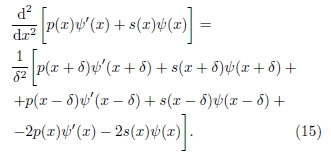
Substituindo as derivadas de primeira ordem pelas aproximações

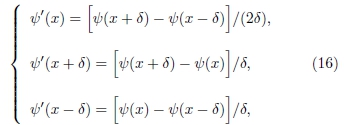
obtém-se

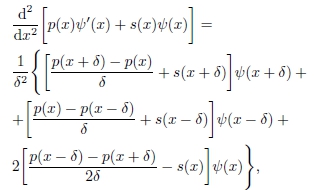
ou seja,

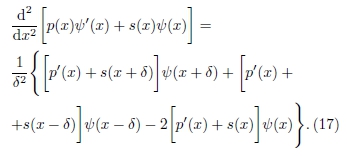
Levando em conta que o lado esquerdo da Eq. (14) é igual a

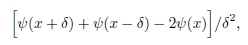
pode-se escrever

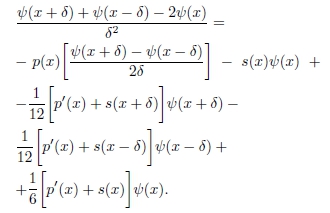
Reagrupando-se os termos, e fazendo-se

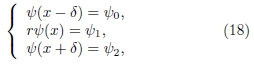
obtém-se a equação de diferenças de Numerov para o problema, adequada à propagação da solução a partir do limites do intervalo de integração

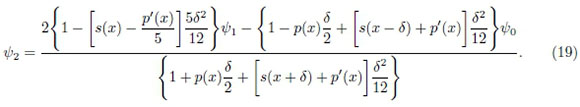
A partir dessa fórmula pode-se implementar um procedimento análogo ao caso anterior para a construção de soluções da equação radial de Schrödinger no intervalo (0,∞).

A Tabela 2 mostra a comparação de alguns dos autovalores (ε) do átomo de hidrogênio, calculados analítica e numericamente para l=1, e a Fig. 4, as correspondentes soluções radiais.

 

 

 

 

5. Comentário final

Os programas para implementar o método de Numerov foram desenvolvidos em C++, para o compilador Cint do ROOT, versão 5.25/2009. Por um problema de espaço, preferimos disponibilizar o código computacional no endereço https://dl.dropboxusercontent.com/u/8500922/numerov_program.pdf.

Embora tenhamos apresentado apenas duas aplicações didáticas, o método de Numerov é suficientemente geral e robusto a ponto de poder ser usado em trabalhos científicos modernos, como a investigação da dependência dos níveis de energia do átomo de hidrogênio não relativístico com a dimensionalidade do espaço [10] ou a análise dos efeitos sobre a dinâmica de uma partícula eletricamente carregada interagindo com um potencial de Chern-Simons em duas dimensões espaciais [11].

 

Referências

[1] Michele Benzi, Key Moments in History of Numerical Analysis, disponível em http://siam.lsu.edu/wp-content/uploads/2009/09/nahist.pdf, acessado em 28/1/2013.         [ Links ]

[2] Peter Lax, apud http://www.dougshaw.com/uhl/.         [ Links ]

[3] Numerov, Boris Vasil'evich. Publications de l'Observatoire Astrophysique Central de Russie II, 188 (1923).         [ Links ]

[4] Boris Vasil'evich Numerov, Monthly Notices of the Royal Astronomical Society 84, 592 (1924).         [ Links ]

[5] Boris Vasil'evich Numerov, Astronomische Nachrichten 230 359 (1927).         [ Links ]

[6] A.C. Allison, Journal of Computational Physics 6, 378 (1970).         [ Links ]

[7] John M. Blatt, Journal of Computational Physics 1, 382 (1967).         [ Links ]

[8] J.P.Leroy and R. Wallace, The Journal of Physical Chemistry 89, 1928 (1985).         [ Links ]

[9] George F. Simmons, Differential Equations: With Applications and Historical Notes (Tata McGraw-Hill, New Dehli, 1974).         [ Links ]

[10] F. Caruso, J. Martins and V. Oguri, Physics Letters A 377, 694 (2013).         [ Links ]

[11] F. Caruso, J.A. Helayël-Neto, J. Martins and V. Oguri, The European Physical Journal B, Condensed Matter Physics, 86, a.n. 324 (2013).         [ Links ]

 

 

Recebido em 20/9/2013
Aceito em 23/11/2013
Publicado em 11/5/2014

 

 

1 E-mail: francisco.caruso@gmail.com
2 Numerical methods have the great virtue that they apply universally. When special methods are introduced to deal with each one of the pitifully small class of [differential] equations that can be handled analytically, students are apt to lose sight of the general idea that every differential equation has a solution and that this solution is uniquely determined by initial data. That today we can use computers to explore the solutions of [differential] equations is truly revolutionary; we are only beginning to glimpse the consequences.
3 A Ref. [6] trata da solução numérica das equações diferenciais acopladas de primeira ordem que resultam da equação de Schrödinger.